Maskestrøm (elektroteknikk)

Maskestrøm er en systematisk metode for å analysere en elektrisk krets. Metoden går ut på å se på maskene i kretsen hver for seg, og sette opp KVL for hver delstrøm/maskestrøm. I utgangspunktet vil en krets med N masker gi oss N KVL-likninger, men i visse definerte tilfeller får vi enten færre eller flere likninger.

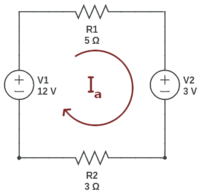
Krets med éi maske

• [math]\displaystyle{ KVL_a: (R_1 + R_2)I_a + V_2 - V_1= 0 }[/math]

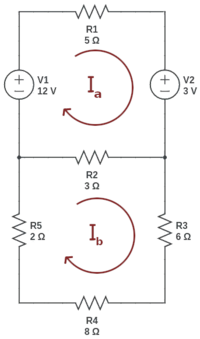
Krets med to masker

• [math]\displaystyle{ KVL_a: (R_1 + R_2)I_a + V_2 - V_1 - R_2I_b = 0 }[/math]
• [math]\displaystyle{ KVL_b: (R_2 + R_3 + R_4 + R_5)I_b - R_2I_a = 0 }[/math]

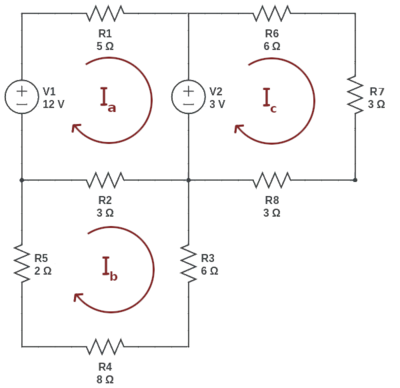
Krets med tre masker

• [math]\displaystyle{ KVL_a: (R_1 + R_2)I_a + V_2 - V_1 - R_2I_b = 0 }[/math]
• [math]\displaystyle{ KVL_b: (R_2 + R_3 + R_4 + R_5)I_b - R_2I_a = 0 }[/math]
• [math]\displaystyle{ KVL_c: (R_6 + R_7 + R_8)I_c - V_2 = 0 }[/math]

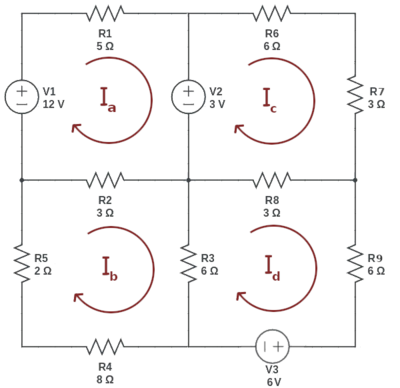
Krets med fire masker

• [math]\displaystyle{ KVL_a: (R_1 + R_2)I_a + V_2 - V_1 - R_2I_b = 0 }[/math]
• [math]\displaystyle{ KVL_b: (R_2 + R_3 + R_4 + R_5)I_b - R_2I_a - R_3I_d = 0 }[/math]
• [math]\displaystyle{ KVL_c: (R_6 + R_7 + R_8)I_c - V_2 - R_8I_d = 0 }[/math]
• [math]\displaystyle{ KVL_d: (R_3 + R_8 + R_9)I_d - R_3I_b - R_8I_c + V_3 = 0 }[/math]

Denne oppgava kan vi bruke som eksempel på løsning vha. matrise. Vi har fire ukjente variabler [math]\displaystyle{ I_a, I_b, I_c, I_d }[/math]. Setter først på form for utvida koeffisientmatrise (ukjente til venstre, konstanter til høyre).

• [math]\displaystyle{ KVL_a: (R_1 + R_2)I_a - R_2I_b + 0I_c + 0I_d = V_1 - V_2 }[/math]
• [math]\displaystyle{ KVL_b: - R_2I_a + (R_2 + R_3 + R_4 + R_5)I_b +0I_c - R_3I_d = 0 }[/math]
• [math]\displaystyle{ KVL_c: 0I_a + 0I_b + (R_6 + R_7 + R_8)I_c - R_8I_d = V_2 }[/math]
• [math]\displaystyle{ KVL_d: 0I_a - R_3I_b - R_8I_c + (R_3 + R_8 + R_9)I_d = -V_3 }[/math]

Setter likningssettet inn i utvida koeffisientmatrise.

[math]\displaystyle{ \left[ \begin{array}{cccc|c} (R_1 + R_2) & - R_2 & 0 & 0 & V_1 - V_2 \\ - R_2 & (R_2 + R_3 + R_4 + R_5) & 0 & - R_3 & 0 \\ 0 & 0 & (R_6 + R_7 + R_8) & - R_8 & V_2 \\ 0 & - R_3 & - R_8 & (R_3 + R_8 + R_9) & -V_3 \\ \end{array} \right] \longrightarrow \left[ \begin{array}{cccc|c} 8 & -3 & 0 & 0 & 9 \\ -3 & 19 & 0 & -6 & 0 \\ 0 & 0 & 12 & -3 & 3 \\ 0 & -6 & -3 & 12 & -6 \\ \end{array} \right] }[/math]

Denne matrisa kan deretter løses for å finne strømmene.